• Główna
• Publikacje
• Prezentacje
• Motyle
• Kontakt

Podwojenie okresu i chaos w hydrodynamicznych modelach Cefeid II populacji

projekt	Iuventus+, IP2012 036572
finansowanie	Ministerstwo Nauki i Szkolnictwa Wyższego, MNiSW
kierownik	Radosław Smolec
termin	06.2013 - 11.2015, zakończony

Przejdź do najważniejsze wyniki, publikacje recenzowane, publikacje konferencyjne oraz prezentacje.

Najważniejsze wyniki

• Podwojenie okresu i inne formy pulsacji w modelach Cefeid II populacji na diagramie HR
  
  

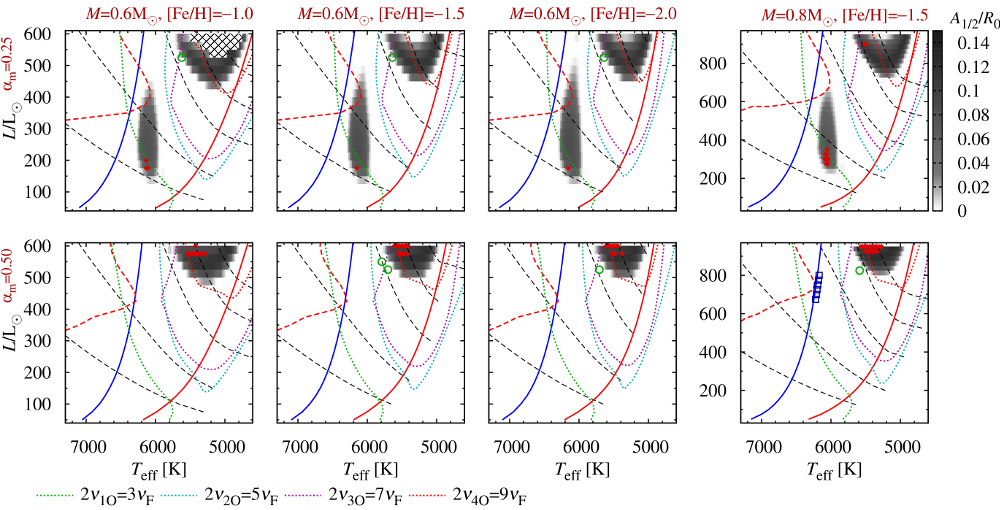
  Rys. 1. Możliwe formy pulsacji dla modeli Cefeid II typu o różnych masach, metalicznościach i parametrach konwektywnych na diagramie HR. W zacienionych obszarach występuje zjawisko podwojenia okresu. Wypełnione romby to modele w których wykryto pulsacje z okresem czterokrotnionym. W modelach oznaczonych otwartymi kółkami obserwujemy okresową modulację pulsacji, zaś modele zaznaczone kwadratami wykazują pulsacje dwumodalne w modzie fundamentalnym i czwartym owertonie. Czarne przerywane linie to linie stałego okresu modu fundamentalnego, od dołu do góry: 2, 4, 8, 12 i 16 dni. Centra kilku rezonansów połówkowych zaznaczono różnymi kropkowanymi liniami, opisanymi w dolnej części rysunku.

  Policzyliśmy duży przegląd nieliniowych konwektywnych modeli Cefeid II Populacji. Modele mają dwie różne wartości masy (0.6M_S i 0.8M_S) oraz trzy wartości metaliczności, [Fe/H]=-1.0, -1.5 oraz -2.0. Dodatkowo, policzyliśmy modele z dwoma zestawami parametrów opisujących turbulentną konwekcję. W modelach znaleźliśmy szereg interesujących form pulsacji, w szczególności:

  • Pulsacje z podwojonym okresem (ang. period-doubling). Taka forma pulsacji obecna jest w dwóch rozłącznych obszarach na diagramie HR - obszary zacienione na szaro na Rys. 1 powyżej. Obszar podwojenia okresu o niższej jasności rozciąga się niemal pionowo, od obszaru modeli typu BL Her do obszaru modeli typu W Vir o krótkich okresach. Okresy pulsacji (niepodwojone) są w zakresie 2-6.5 dni. Jest to ten sam obszar jak znaleziony w promienistych rachunkach przez Buchlera i Moskalika (1992, ADS). Na podstawie tych rachunków, autorzy przewidzieli istnienie gwiazd typu BL Her z podwojeniem okresu, co znalazło potwierdzenie 20 lat później. Efekt został odkryty w gwieździe OGLE-BLG-T2CEP-279 (Soszyński i in. 2011, ADS, Smolec i in. 2012, ADS). Drugi obszar podwojenia okresu rozciąga się dla wyższych jasności, w obszarze gwiazd typu W Vir (P>9.5 dni).
  • Pulsacje z okresem czterokrotnionym; wykryte w kilku modelach wewnątrz obszarów podwojenia okresu. Na Rys. 1 modele te zaznaczone są rombami. Taka forma pulsacji jeszcze nie została zaobserwowana w Cefeidach II populacji.
  • Modulacja pulsacji; obecna w kilku modelach zaznaczonych na Rys. 1 kółkami. Modulacja ma niską amplitudę, występuje w bardzo wąskich (~10K) obszarach na diagramie HR. Wszystkie modele są typu W Vir, okresy pulsacji są rzędu 9-10 dni, okresy modulacji są kilka-kilkanaście razy dłuższe.
  • Pulsacje dwumodalne, w modzie fundamentalnym oraz w czwartym owertonie; znalezione w modelach zaznaczonych na Rys. 1 kwadratami. Modele te przedstawione są bliżej w następnym punkcie.

  W modelach nie znaleźliśmy zachowań chaotycznych podobnych do tych z poprzedniej pracy (Smolec i Moskalik 2012; obecne modele są bardziej realistyczne, przyjęto inne parametry modelu konwekcji). Przegląd modeli jest ograniczony w jasności; modeli najjaśniejszych nie udało się policzyć, z uwagi na niestabilność dynamiczną (odrywanie się zewnętrznych warstw modeli). Pełne wyniki przedstawiono w pracy w MNRAS (PDF, arXiv:1512.01550).

• Pulsacje dwumodalne, w modzie fundamentalnym i czwartym owertonie (mod powierzchniowy)
  
  

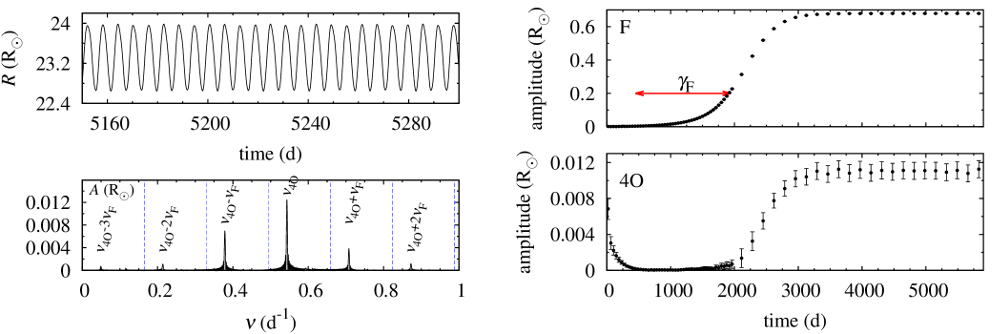
  Rys. 2. Panel górny lewy: zmiana promienia w czasie dla modelu dwumodalnego F+4O; Panel dolny lewy: widmo częstości po usunięciu (prewhiteningu) modu fundamentalnego i częstości harmonicznych (niebieskie przerywane linie); Panele prawe: zmiana amplitudy modu fundamentalnego (górny prawy) oraz czwartego owertonu (dolny prawy) podczas początkowego etapu całkowania modelu.

  W przeglądzie modeli Cefeid II populacji znaleźliśmy bardzo interesującą formę pulsacji: pulsacje dwumodalne w modzie fundamentalnym oraz w czwartym owertonie (modele zaznaczone kwadratami na Rys. 1). Czwarty owerton jest tzw. modem powierzchniowym lub złapanym; amplituda pulsacji jest wysoka tylko w warstwach zewnętrznych, pomiędzy powierzchnią, a obszarami częściowej jonizacji wodoru (w literaturze spotyka się również określenie mody dziwne, ang. strange modes, np. Buchler i in. 1997, ADS). Chociaż liniowe tempo narastania dla czwartego owertonu jest ujemne, mod ten jest słabo tłumiony, w porównaniu z sąsiednimi, niezłapanymi modami owertonowymi. W policzonych modelach amplituda czwartego owertonu jest niska; w krzywej zmiany promienia (górny lewy panel na Rys. 2) tzw. dudnienie dwóch wzbudzonych częstości jest ledwo zauważalne. Obecność czwartego owertonu jest ewidentna w widmie częstości (dolny lewy panel na Rys. 2). Taka forma pulsacji znaleziona została jedynie w modelach bardziej masywnych, przylegających do niebieskiej granicy ścieżki niestabilności (Rys. 1). Okresy modu fundamentalnego są w zakresie 5.6-6.8 dni, stosunek okresów wzbudzonych modów, P_4O/P_F, wynosi około 0.3. Czwarty owerton jest lekko tłumiony co widać na rysunku 2 w dolnym prawym panelu: jego amplituda spada eksponencjalnie w początkowej fazie całkowania modelu i zaczyna narastać dopiero gdy amplituda modu fundamentalnego (górny prawy panel) staje się duża. Pomimo ujemnego liniowego tempa narastania czwartego owertonu, dwumodalność ma najpewniej charakter nierezonansowy. Bardziej szczegółowa analiza jest jednak niezbędna i zaplanowana. Przeczytaj więcej w artykule w MNRAS (PDF, arXiv:1512.01550).

• Chaos w modelach gwiazd typu BL Herculis

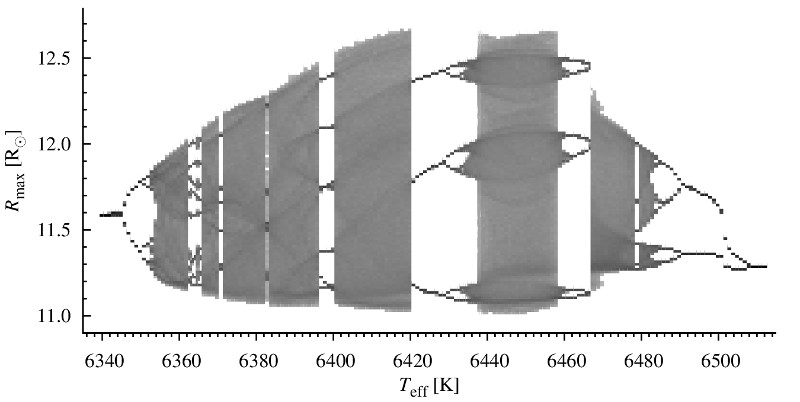
W ciągu hydrodynamicznych modeli gwiazd typu BL Herculis (L=const, M=const, T_eff zmieniana) znaleźliśmy różnorodne zachowania dynamiczne charakterystyczne dla deterministycznego chaosu. Rysunek powyżej to diagram bifurkacyjny dla tych modeli. Pokazuje on możliwe wartości maksymalnego promienia modelu w czasie, R_max, w funkcji temperatury efektywnej modelu. Wiele zjawisk zaobserwowano po raz pierwszy w kontekście gwiazd pulsujących. Zaobserwowaliśmy różne drogi prowadzące do chaosu (kaskada podwojenia okresu, intermitencja), kryzys atraktora chaotycznego, domeny stabilnych, okresowych pulsacji wewnątrz domen chaotycznych, intermitencję typów pierwszego i trzeciego.

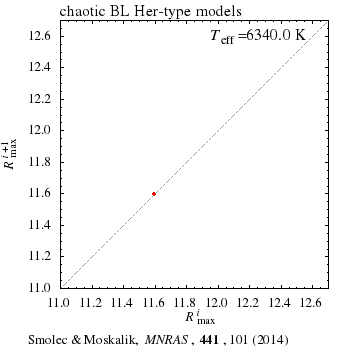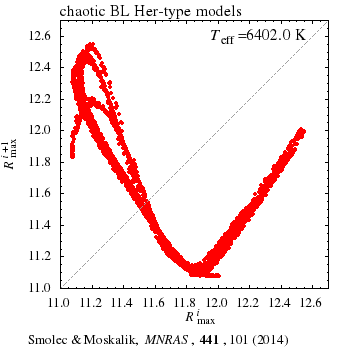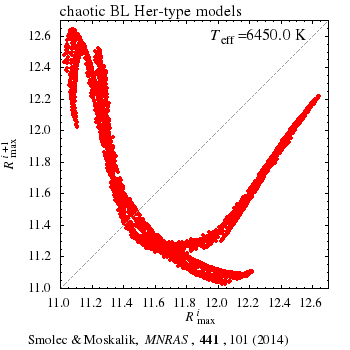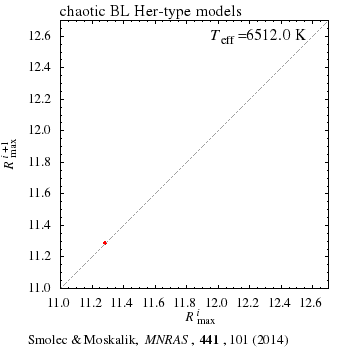
Hydrodynamiczne modele gwiazd typu BL Her są jakościowo podobne do innych znanych układów fizycznych wykazujących chaos. Odnajdujemy bliskie podobieństwo pomiędzy własnościami naszych modeli a nawet najprostszym układem chaotycznym, iterowaniem mapy logistycznej: x_i+1=kx_i(1-x_i). Poniższe animacje pokazują: (lewa) pierwszą mapę powrotną dla równania logistycznego (wykres x_i+1 vs. x_i, w funkcji parametru k), oraz (prawa) pierwszą mapę powrotną dla maksymalnych wartości promienia w modelach BL Her (wykres R_maxⁱ⁺¹ vs. R_maxⁱ w funkcji T_eff). Więcej w informacji w pracy w czasopiśmie MNRAS (PDF, arXiv:1403.4937).

Publikacje recenzowane

• Smolec, R.; Survey of non-linear hydrodynamic models of type-II Cepheids; MNRAS, 456, 3475 (2016); PDF, arXiv:1512.01550
• Smolec, R., Moskalik, P.; Chaos in hydrodynamic BL Herculis models; MNRAS, 441, 101 (2014); PDF, arXiv:1403.4937

Publikacje konferencyjne

• Smolec, R.; Nonlinear convective pulsation models of type II Cepheids, Astronomy in Focus, XXIXB, E15 (2016); doi; Proc. of the IAU General Assembly XXIX, Focus Meeting 17: Advances in Stellar Physics from Asteroseismology, Honolulu, 3-14 sierpnia 2015; www
• Smolec, R.; Dynamical phenomena in the pulsation of type-II Cepheid models, in Mem. Soc. Astron. It., 87, 311-314 (2016); EWASS2015, Tenerife, 22-26 June 2015; www
• Smolec, R., Moskalik, P.; Order and chaos in hydrodynamic BL Her models, w Proc. of the Polish Astron. Soc., 1, 154-156 (2014); XXXVI Polish Astronomical Society Meeting, Warszawa, 11-15 września; 2013; www
• Smolec, R., Moskalik, P.; Chaos in hydrodynamic models of pulsating BL Her-type stars; w 7th CHAOS Conference Proceedings, p. 471-479 (2014); The 7th Chaotic Modeling and Simulation International Conference, Lizbona, 7-10 czerwca 2014; www
• Smolec, R., Moskalik, P.; Order and chaos in hydrodynamic BL Her models; IAUS 301, p. 489 (2014); arXiv:1309.5962; IAU Symposium No. 301: Precision Asteroseismology: Celebration of the Scientific Opus of Wojtek Dziembowski, Wrocław, 19-23 sierpnia 2013; www

Prezentacje

---