Tidal deformability and other global parameters of compact stars
Motivated by the GW170817 event, we have published a study on tidal deformabilities of neutron stars with equations of state that feature substantial (strong, meaning destabilising) phase transitions:
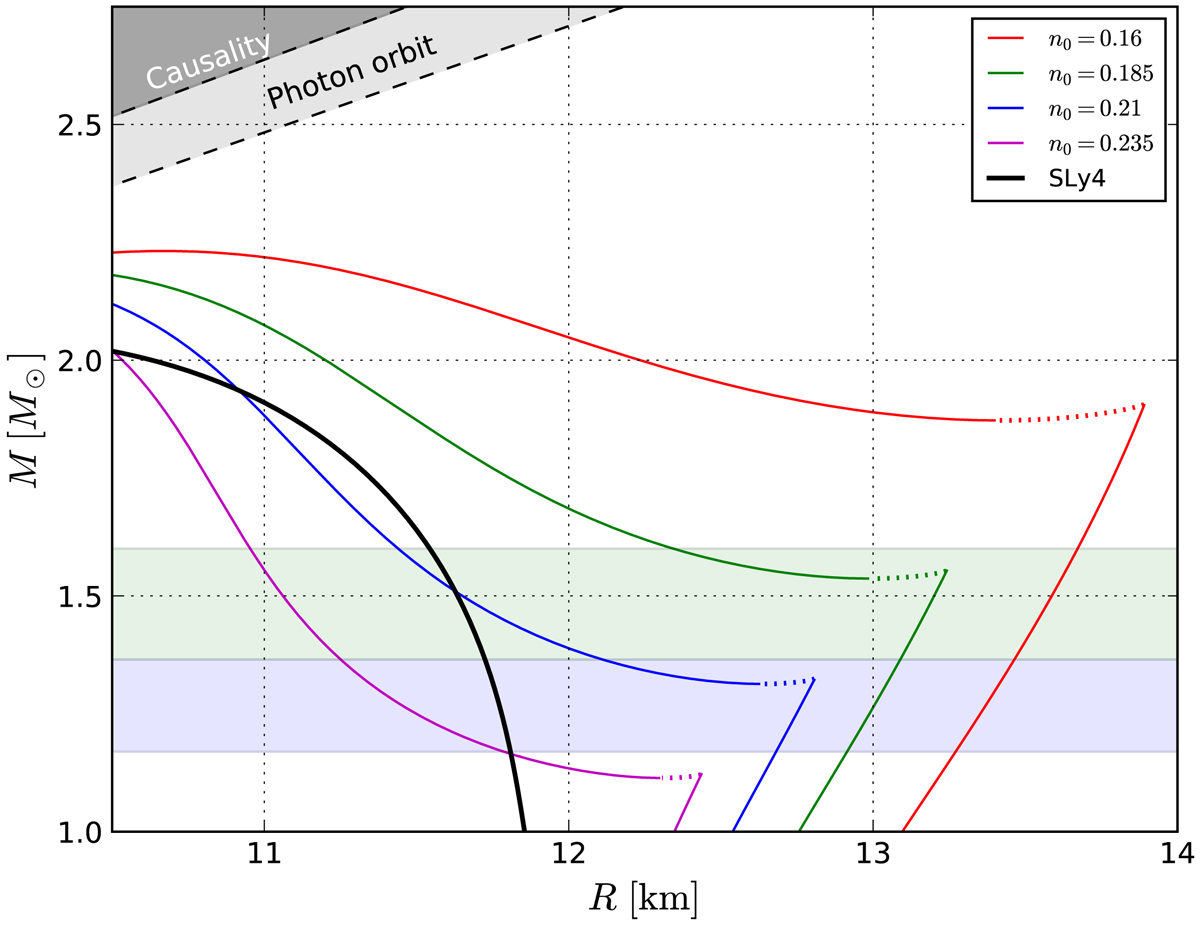
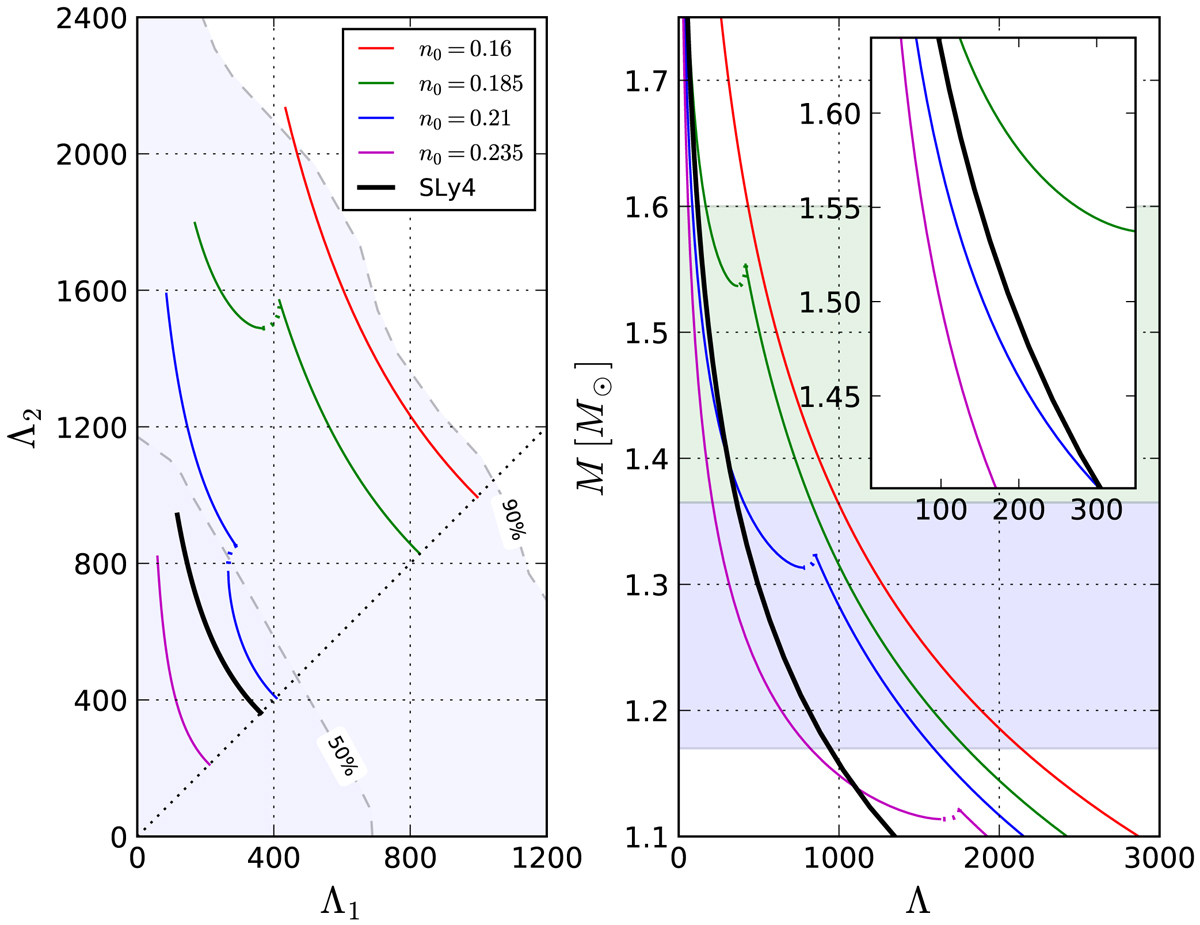
Using parametric equations of state (relativistic polytropes and simple > quark bag model) to model dense-matter phase transitions, we study global, measurable astrophysical parameters of compact stars, such as their allowed radii and tidal deformabilities. We also investigate the influence of stiffness of matter before the onset of the phase transitions on the parameters of the possible exotic dense phase. The aim of our study is to compare the parameter space of the dense matter equation of state permitting phase transitions to a sub-space compatible with by current observational constraints, such as the maximum observable mass, tidal deformabilities of neutron star mergers, radii of configurations before the onset of the phase transition, and to give predictions for future observations. We study solutions of the Tolman-Oppenheimer-Volkoff equations for a flexible set of parametric equations of state, constructed using a realistic description of neutron-star crust (up to the nuclear saturation density), and relativistic polytropes connected by a density-jump phase transition to a simple bag model description of deconfined quark matter. In order to be consistent with recent observations of massive neutron stars, a compact star with a strong phase transition cannot have a radius smaller than 12 km in the range of masses $1.2 - 1.6\,M_\odot$. We also compare tidal deformabilities of stars with weak and strong phase transitions with the results of the GW170817 neutron star merger. Specifically, we study characteristic phase transition features in the $\Lambda_1-\Lambda_2$ relation, and estimate the deviations of our results from the approximate formulæ for $\tilde{\Lambda}-R(M_1)$ and $\Lambda$-compactness, proposed in the literature. We find constraints on a hybrid equations of state to produce stable neutron stars on the twin branch. For the exemplary equation of state most of the high-mass twins can be formed for the minimal values of the density jump $\lambda = 1.33-1.54$ and corresponding values of the square of the speed of sound $\alpha = 0.7-0.37$. We compare results with gravitational waves observations, as well as with the theoretical causal limit and find out that the more favorable equations of state have phase transition point at the baryon density around $0.34-0.51$ [fm$^{-3}$]. We also show, that minimal radius that can be produced on a twin branch is between 9.5 and 10.5 km.
Authors from CAMK: Magdalena Sieniawska, Michał Bejger, Leszek Zdunik.
