Neural networks reconstruction of the dense-matter equation of state from neutron-star parameters
Our recent work describes a ML algorithm teaching process to reconstruct the dense-matter equation of state, used to build a structure of neutron stars, from simulated observations of neutron stars: their gravitational masses $M$, radii (from the EM observations) as well as tidal deformabilities $\Lambda$ (first observed in the GW170817 event).
We have trained a neural network on a set of artificial equations of state (piecewise relativistic polytropes) and are able to demonstrate that the network can recover realistic microphysical equations of state - this means that the network can generalize the concept.
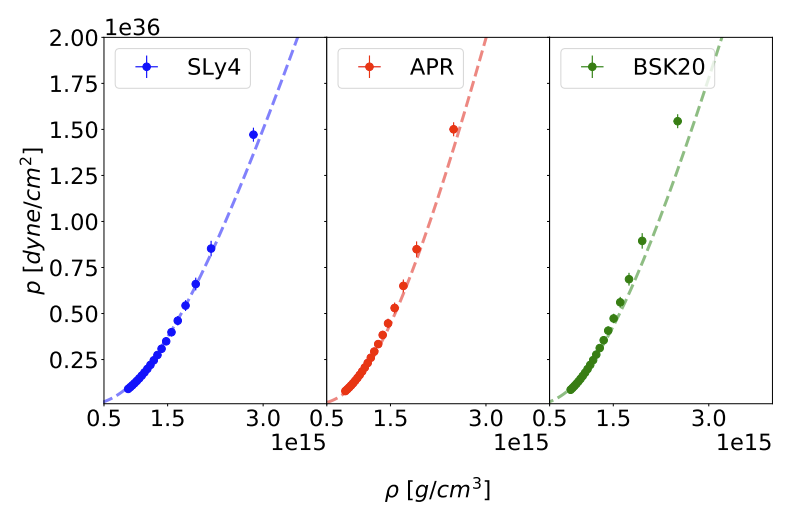
We have also checked that one can infer radius, which is not directly measured by gravitational-wave detectors, from the tidal deformability measurements. It works very well with a relatively simple artificial neural network. The complete abstract is as follows:
The aim of this work is to study the application of the artificial neural networks guided by the autoencoder architecture as a method for precise reconstruction of the neutron star equation of state, using their observable parameters: masses, radii and tidal deformabilities. In addition we study how well the neutron star radius can be reconstructed using the gravitational-wave only observations of tidal deformability, i.e. quantities which are not related in a straightforward way. Application of artificial neural network in the equation of state reconstruction exploits the non-linear potential of this machine learning model. Since each neuron in the network is basically a non-linear function, it is possible to create a complex mapping between the input sets of observations and the output equation of state table. Within the supervised training paradigm, we construct a few hidden layer deep neural network on a generated data set, consisting of a realistic equation of state for the neutron star crust connected with a piecewise relativistic polytropes dense core, with parameters representative to the state-of-the art realistic equations of state. We demonstrate the performance of our machine learning implementation with respect to the simulated cases with varying number of observations and measurement uncertainties. Furthermore we study the impact of the neutron star mass distributions on the results. Finally, we test the reconstruction of the equation of state trained on parametric polytropic training set using the simulated mass–radius and mass–tidal-deformability sequences based on realistic equations of state. Neural networks trained with a limited data set are able to generalize the mapping between global parameters and equation of state input tables for realistic models.
Update 29.06.2020: just accepted by the A&A!
