| id | P | PB | A1 | Am/A1 | R | Q | remarks | animations |
|---|---|---|---|---|---|---|---|---|
| OGLE-BLG-RRLYR-06134 | 0.63490732(4) | 46.022(2) | 0.229 | 0.135 | 0.574 | -0.271 | R21-A1, R31-A1, φ21-A1, φ31-A1, φ21-R21 | |
| OGLE-BLG-RRLYR-07576 | 0.61862594(8) | 121.77(2) | 0.127 | 0.160 | 2.824 | 0.477 | R21-A1, R31-A1, φ21-A1, φ31-A1, φ21-R21 | |
| OGLE-BLG-RRLYR-09131 | 0.52041652(4) | 37.776(1) | 0.236 | 0.135 | 1.428 | 0.176 | BL+ or mod | R21-A1, R31-A1, φ21-A1, φ31-A1, φ21-R21 |
| OGLE-BLG-RRLYR-10041 | 0.54659603(5) | 143.07(2) | 0.177 | 0.156 | 1.400 | 0.168 | R21-A1, R31-A1, φ21-A1, φ31-A1, φ21-R21 | |
| OGLE-BLG-RRLYR-09909 | 0.6016087(1) | 57.642(4) | 0.117 | 0.384 | 13.989 | 0.867 | BL+, mod | R21-A1, R31-A1, φ21-A1, φ31-A1, φ21-R21 |
| OGLE-BLG-RRLYR-09450 | 0.48346952(1) | 78.158(5) | 0.243 | 0.154 | 0.936 | -0.033 | 1O, HIF | R21-A1, R31-A1, φ21-A1, φ31-A1, φ21-R21 |
| OGLE-BLG-RRLYR-10182 | 0.6130059(2) | 86.28(1) | 0.072 | 0.366 | 20.455 | 0.907 | BL+ or mod | R21-A1, R31-A1, φ21-A1, φ31-A1, φ21-R21 |
| OGLE-BLG-RRLYR-10044 | 0.7906896(2) | 89.41(2) | 0.117 | 0.174 | 17.253 | 0.890 | - | R21-A1, R31-A1, φ21-A1, φ31-A1, φ21-R21 |
| OGLE-BLG-RRLYR-09596 | 0.60166396(5) | 96.55(3) | 0.149 | 0.042 | 0.862 | -0.074 | - | R21-A1, R31-A1, φ21-A1, φ31-A1, φ21-R21 |
| OGLE-BLG-RRLYR-09098 | 0.6010593(1) | 57.70(1) | 0.121 | 0.146 | 11.857 | 0.844 | - | R21-A1, R31-A1, φ21-A1, φ31-A1, φ21-R21 |
| OGLE-BLG-RRLYR-08950 | 0.50334874(2) | 109.15(2) | 0.231 | 0.079 | 0.654 | -0.209 | HIF? | R21-A1, R31-A1, φ21-A1, φ31-A1, φ21-R21 |
| OGLE-BLG-RRLYR-07538 | 0.47330144(5) | 176.32(6) | 0.213 | 0.109 | 0.957 | -0.022 | - | R21-A1, R31-A1, φ21-A1, φ31-A1, φ21-R21 |
| OGLE-BLG-RRLYR-06671 | 0.56614361(7) | 87.78(2) | 0.128 | 0.109 | 3.126 | 0.515 | - | R21-A1, R31-A1, φ21-A1, φ31-A1, φ21-R21 |

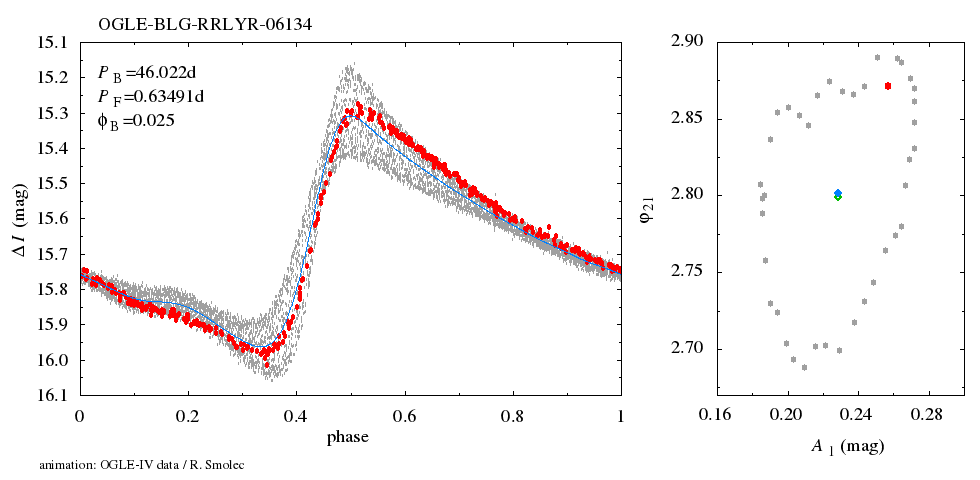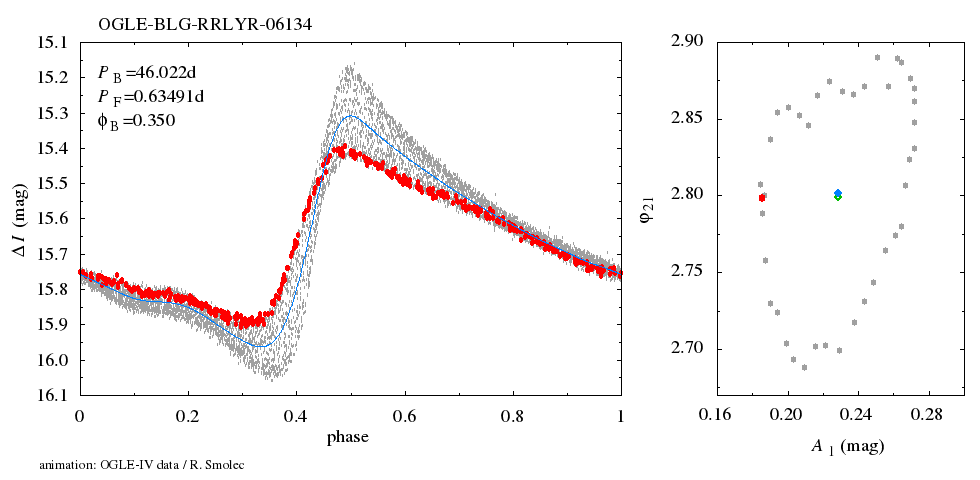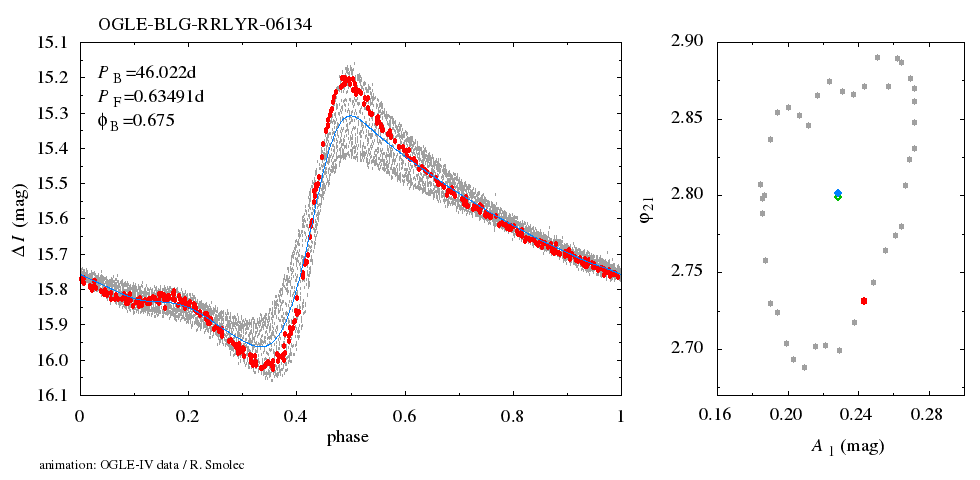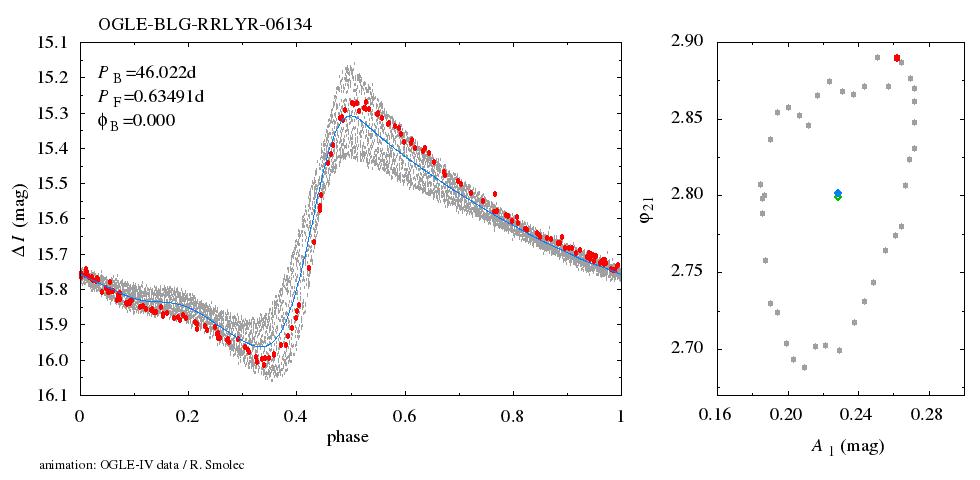
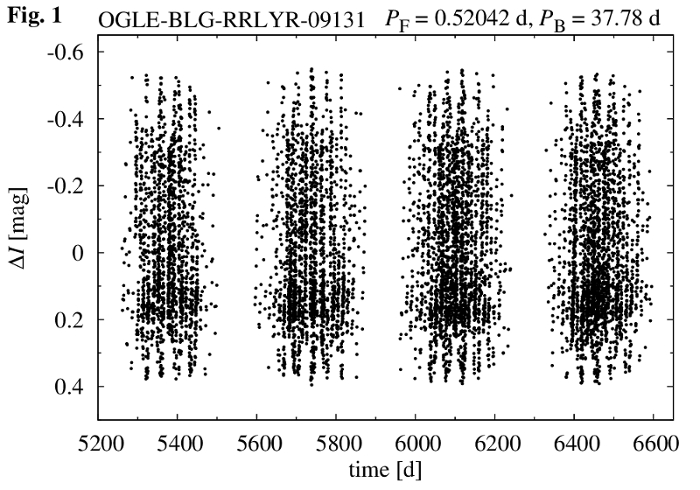
We illustrate the process with the help of OGLE-BLG-RRLYR-09131. Its I-band photometric data are plotted in Fig. 1.
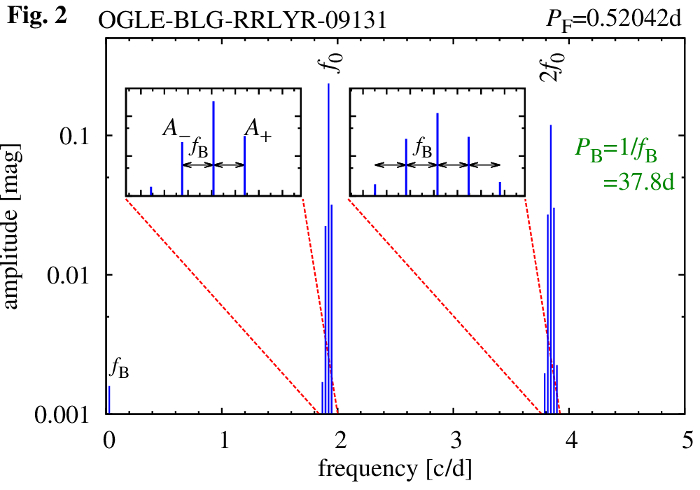
First we compute the discrete Fourier transform of the data. The resulting frequency spectrum allows us to estimate the pulsation frequency, \(f_0\), and modulation frequency, \(f_{\rm B}\). In the frequency spectrum, modulation reveals through equidistant multiplet structures centered at the pulsation frequency and its harmonics. Separation between the multiplet components corresponds to modulation frequency and its inverse corresponds to the modulation period. In Fig. 2 we present the schematic frequency spectrum for 09131 illustrating the multiplet structures at \(f_0\) and \(2f_0\).
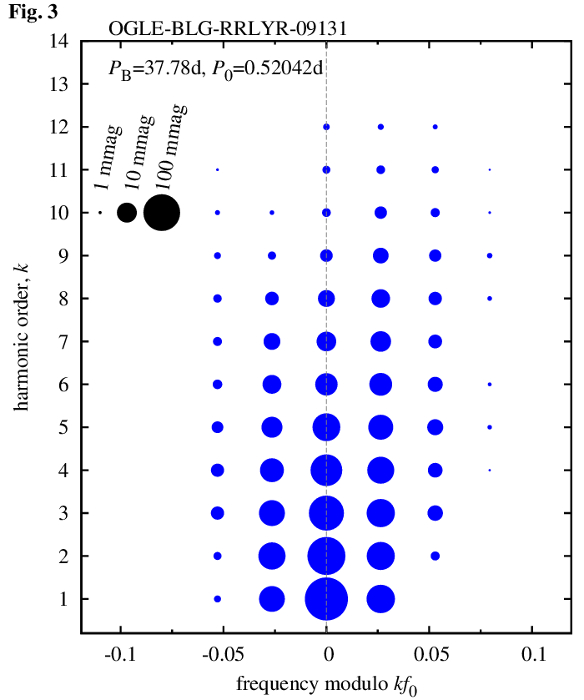
All multiplet components detected in the frequency spectrum, are conveniently illustrated with the help of an echelle diagram (see e.g. Guggenberger et al., 2012) plotted in Fig. 3 below. Frequency of the detected peaks, \(f\), is ploted versus \(f\) modulo \(kf_0\).
Now we phase the data displayed in Fig. 1 with the modulation period. The resulting modulation curve is displayed in Fig. 4 below.
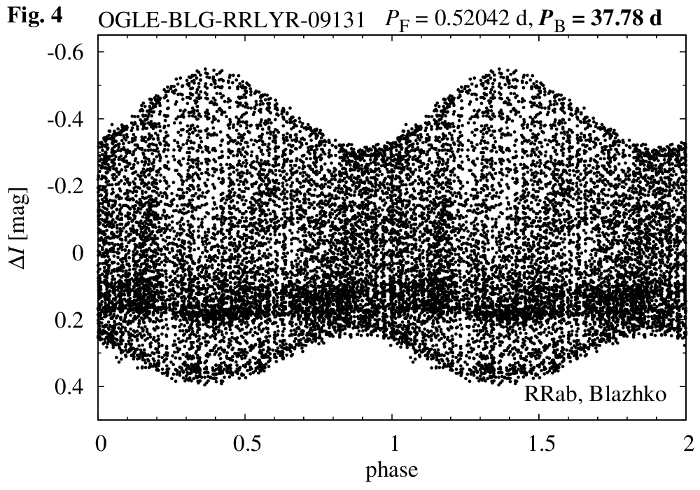
The procedure is straightforward now. We divide the data displayed in Fig. 4 into 40 (overlapping) bins, each 0.05 wide, corresponding to different phases of the modulation cycle. These data form a basis for a single frame of the animation. They are folded with the pulsation period to get the temporary pulsation light curve. Animation, composed of 40 such snapshots, shows how the light curve changes over the modulation cycle.
In the left panel of the animation, light curve change over the modulation cycle is displayed. Red points correspond to a temporary snapshot. The background, a band of grey points, is formed by all data folded with the pulsation period (mean pulsation light curve). Blue curve is a Fourier fit to the extracted light curve. In the right panel, the variation of various Fourier decomposition parameters over the Blazhko cycle is displayed. Filled blue and open green diamonds, correspond to the Fourier parameters of the extracted and mean light curves, respectively.
The pulsation light curve of non-modulated RR Lyrae stars is commonly described with the Fourier series of the following form:
$$ m(t)=m_0+\sum_{k=1}^N A_k\sin(2\pi k f_0 t+\varphi_k) $$
Frequency, \(f_0\), amplitudes, \(A_k\), and phases, \(\varphi_k\), are adjusted using non-linear least-square fit. To get the mean light curve, we fit the above Fourier series to all data. The above equation is not a good representation of the data for modulated stars, however. A much better solution includes the modulation multiplets (Figs. 2 and 3):
\begin{align}
m(t)=m_0&+\sum_{k=1}^N A_k\sin(2\pi k f_0 t+\varphi_k)\\
&+\sum_{k=1}^N A_k^+\sin\big[2\pi( k f_0+f_B) t+\varphi_k^+\big]\\
&+\sum_{k=1}^N A_k^-\sin\big[2\pi( k f_0-f_B) t+\varphi_k^-\big]
\end{align}
Above, for simplicity, only triplet components were included. With such solution fitted to the data, one can filter out the modulation. The resulting data, folded with the pulsation period, are called extracted light curve.
Once Fourier series is fitted to the data, the Fourier decomposition parameters, amplitude ratios, \(R_{k1}\), and phase differences, \(\varphi_{k1}\), are computed as follows (Simon & Lee, 1981):
$$R_{k1}=\frac{A_k}{A_1},\quad\varphi_{k1}=\varphi_k-k\varphi_1$$
\(P\) and \(P_{\rm B}\) are pulsation and modulation (Blazhko) periods, respectively. They can be estimated with the help of Fourier transform as described above. \(A_1\) is amplitude of the fundamental mode (height of the peak at \(f_0\) in Fig. 2). \(A_{\rm m}/A_1\) estimates the amplitude of the modulation. \(A_{\rm m}\) is the amplitude of the highest modulation peak at \(f_0\) (see Fig. 2). \(R\) and \(Q\) characterize the asymmetry of the side peaks. They are computed using the amplitudes of the modulation side peaks (see Fig. 2), using the following formulae:
$$R=\frac{A_{+}}{A_{-}},\quad Q=\frac{A_+-A_-}{A_++A_-}$$
 Questions and comments: smolec AT camk.edu.pl
Questions and comments: smolec AT camk.edu.pl