Research
interests
Recent projects
Seminar talks
Modelling the energy spectra
of X-ray quasi-periodic oscillations
Zycki & Sobolewska, 2005, MNRAS, 364, 891, (ADS, astro-ph/0509221)
(See also a seminar
talk I gave at SLAC in August 2005)
|
QPO are a common phenomenon in
X-ray binaries. They come in a number of “flavours”,
with interesting correlations between their frequencies (and this
includes QPO in cataclysmic variables, i.e. systems with
accreting white dwarfs!). QPO attract a lot of attention because
they point to an existence of fairly precise “clocks”
in those systems, even though most of the variability power is in
the form of a broad band (i.e. aperiodic) noise. Probably because
of those “clocks”, most of the work done on QPO,
concentrated on their frequencies. On the theory side, almost all
models invoke oscillations of the standard, optically thick disk.
The problem is, it is hard X-rays
that are being modulated, and it is far from
obvious that any oscillations of the optically thick disk (which
emits ~1 keV thermal radiation), can be responsible for hard
X-ray QPO.
Just as usual energy spectra
are a signature of the processes generating the X-rays, QPO
energy spectra (which are, simply, the r.m.s.(E) spectra) should
tell us something on how the QPO are generated.
Assume that hard X-rays are
produced in inverse Compton process (most people would agree with
that). Then, the processes going on in the emitting plasma cloud,
and the emitted spectrum, are described by
two main parameters: the rate of heating
the plasma (which includes both thermal heating and
injection of energetic particles), and the
rate of cooling, which is the luminosity (compactness) of
soft photons (there are some other less important parameters)
(see very good description of these processes in Paolo Coppi's
article).
Make one more assumption: that
the QPO is a real modulation of the luminosity of emitted X-rays,
rather that an “apparent” effect related to, for
example, relativistic Doppler effect (as we did here).
Then, irrespectively of the physical mechanism of QPO, there
is not much choice as to what can be modulated: it must be one of
the parameters which actually describe the spectrum of
Comptonized radiation – the heating rate, or the cooling
rate.
|
|
|
|
Now, assume that the heating
rate of a plasma cloud is modulated periodically, while the
cooling rate stays constant. Computing a sequence of spectra we
get harder spectra when the ratio
heating/cooling is larger, and softer
spectra when the ratio is smaller. In other words, we
obtain a specific pattern of spectral
variability. The spectral variability produces
a r.m.s.(E) relation, describing the amplitude of the
variability as a function of energy. In this case the r.m.s.
increases with energy, and the reason for this should be obvious
from the plot to the right.
|
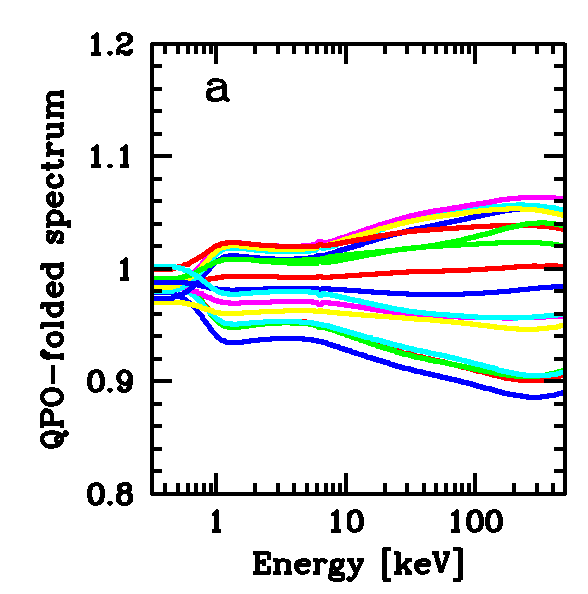
|
|
|
QPO period-folded
spectra, divided by the time averaged spectrum. Amplitude of
variability increases with energy.
|
|
|
|
|
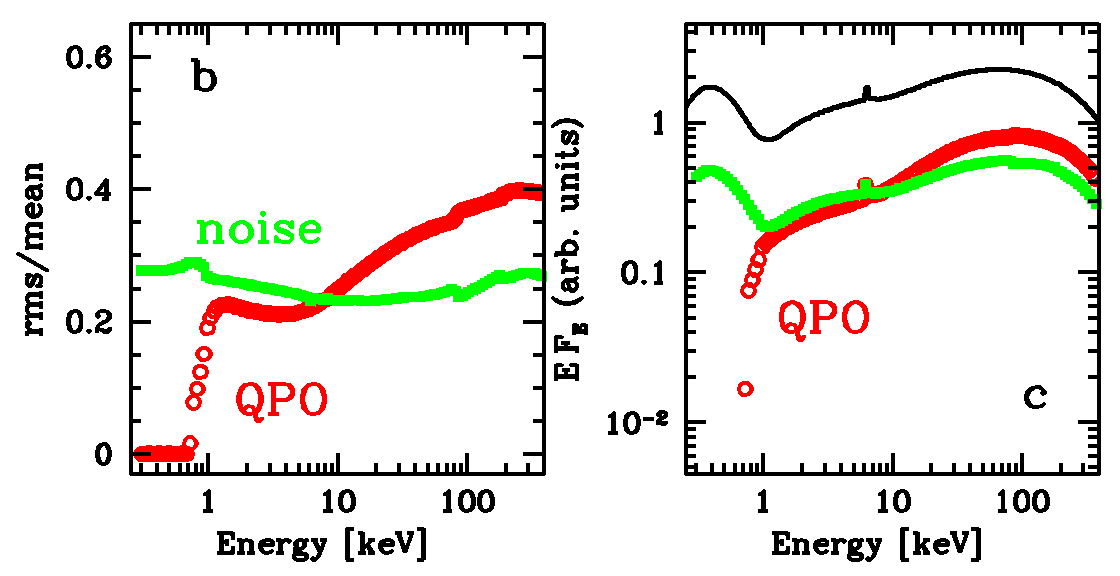
|
Corresponding r.m.s.(E)
relation is shown to the left (left panel). When multiplied by
time-averaged spectrum, this gives something that can be thought
of as the QPO energy spectrum. The important result here is that
te QPO energy spectrum is harder than the time averaged spectrum.
|
|
|
|
|
One can compute many other
observable quantities, for example results of cross-correlation
analysis between two different energy bands, to see if any
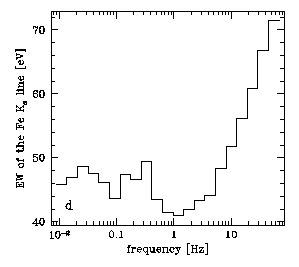
features appear at the frequency of the QPO (here at 1 Hz). In
this example, there is a local maximum in the equivalent width of
the Fe Kalpha line, and the time lags between 3 and 9 keV
lightcurves show rather complex behaviour around 1 Hz.
|
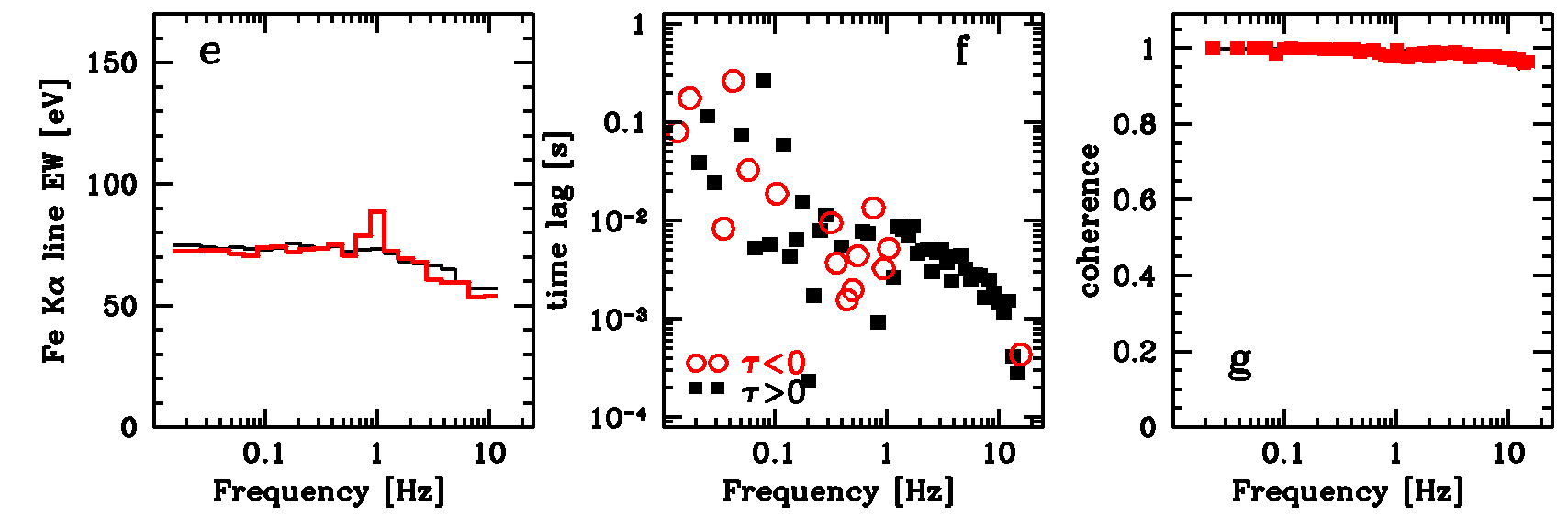
|
|
|
|
|
One can consider a
number of other possibilities for producing the modulations.
Modulation of the
cooling rate (with or without temperature modulation)
Modulation of the
amplitude of reflection
Each of these will
produce a specific pattern of spectral variability, and, as a
consequence, QPO r.m.s. spectra.
|
|
|
top
Influence of relativistic
effects on X-ray variability of accreting black holes
Zycki & Niedzwiecki,
2005, MNRAS, 359, 308: astro-ph
(color .ps, .pdf), ADS,
pdf (b&w)
|
Imagine
magnetic flares as the source of X-ray emission in accreting
black holes. Actually, this is what we think is happening at high
accretion rates. (“High” means here “too high
for the cold disk to remain truncated far away from the black
hole”, but it is hard to give one good number; let's say
it's a few per cent of Eddington rate.) The
magnetic flares rotate with the accretion disk, so the X-rays are
modulated by relativistic effects. The
main effect is obviously the Doppler effects, which enhance the
emission from the part of the disk, which is going
towards us, but reduce the emission from flares going
away from us. Now, you've read this argument many times,
but in most cases it was in connection with the broad profile of
Fe Kalpha line, right? But the emission (both primary and
reprocessed) is modulated in time,
so what would we see, if we could observe the X-rays at
sufficiently high time resolution?
This question
was actually answered quite a few times in the past, in somewhat
different contexts (Bardeen, Cuningham in the 1970s, Abramowicz
and collaborators in 1980s).
|

|
|
|
|
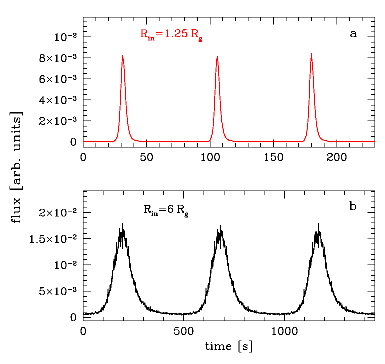
So,
how does the time modulation look like? We computed the
modulation of an intrinsically constant signal, emitted at 1.25
Rg (very close to the last stable orbit in extreme
Kerr metric) and 6 Rg, as seen at 60 degrees
inclination, for 106 MSun (this sets the
timescale). Below, on the left are the lightcurves, on the right
– power spectra. The modulation is very strong, you cannot
fail to notice it. Of course, it is periodic but far from
sinusoidal, so there is a lot of harmonics in the PDS
|
|
|
|
|
Of
course, in a realistic situation we are not dealing with a single
flare. We assume there is a lot of flares, longer and shorter (as
required to explain the broad band power spectra in the flare
avalanche model of Poutanen
& Fabian 1999). Their radial distribution is such that
the energy emitted follows the formula for an accretion disk
around a Kerr black hole with a=0.998 – meaning simply that
they are concentrated toward the center. All flares follow
Keplerian orbits. After some time (about 106 sec here)
you see something like in the picture to the right: red means
weak emission, green blue, cyan, magenta, yellow –
progressively more (in log scale). The flares usually last longer
than the orbital period (this is a requirement for the flare
avalanche model; is it possible physically??), so each flare is
modulated many times by the relativistic effects.
|
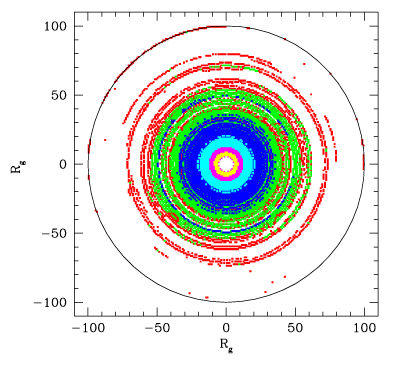
|
|
|
|
|
Compare the
lightcurves: below, directly from the flare
model, no relativistic effects, and right, with
the relativistic effects included. The modulation adds a
lot of power at high Fourier frequency.
|
|
|
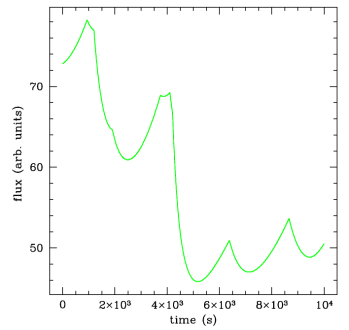
|
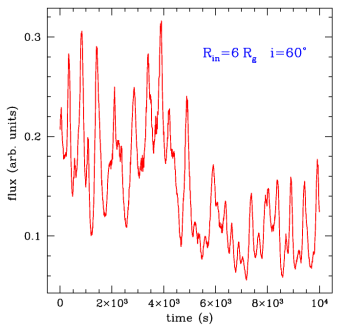
|
|
|
|
|
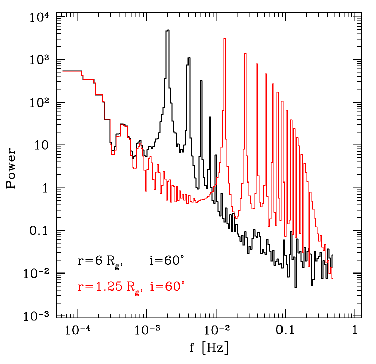
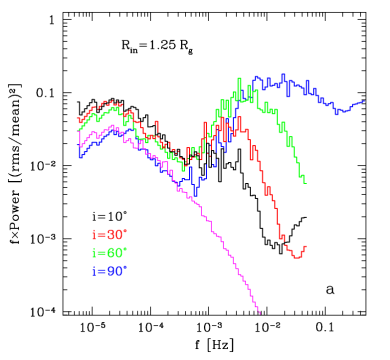
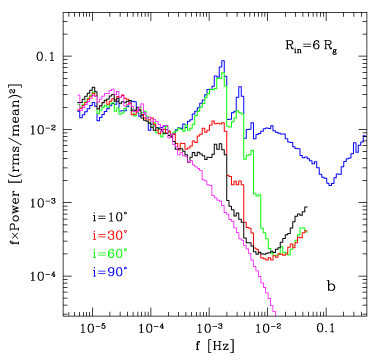
And
here come our main results:
power spectra of such modulated signals.
|
|
|
|
The signal is
rather obvious, isn't it? The magenta curve
shows PDS of the intrinsic signal, without relativistic
modulation. Of course, the modulation is stronger at higher
inclinations. For Rin=1.25 Rg, it has so many harmonics that it
all blends into a big bump, without any clear sharp peak. For
Rin= 6 Rg you see peaks corresponding to the main frequency and
one or two harmonics, at the innermost radius.
Would
this be seen in real observations? Yes, it would. We simulated
the data corresponding to recent XMM-Newton observations of
MCG-60-30-15 (Vaughan et al. 2003) – count rate, duration,
black hole mass 106 MSun, inclination 30 degrees. And
the modulation would be more than obvious in such data, if it
was there. But it is not! Read
more in our paper, how we did the simulations, and what exactly
are the results.
|
top
Variability of the Ka line in
accreting black holes
(Zycki
2004, MNRAS, 351, 1180)
|
This is
basically a continuation of these two previous projects: fourier,
fevar. This time I concentrate on the
variability of the iron Kalpha line in
the cold disk plus hot flow (“disrupted
disk”) geometry. One one hand, this is
motivated by those papers reporting that the Kalpha line in AGN
is generally less variable that the continuum which drives it's
emission, and it does not seem to correlate well with its driving
continuum. On the other hand, it seems that we see an equivalent
effect in Cyg X-1 and other black hole binaries: in the Fourier
frequency resolved spectra the amplitude of reflection the EW of
the Kalpha line get smaller with increasing Fourier frequency.
Which means that the reprocessed component responds to the
continuum variability on long time scales, but it does not do so
on short time scales.
|
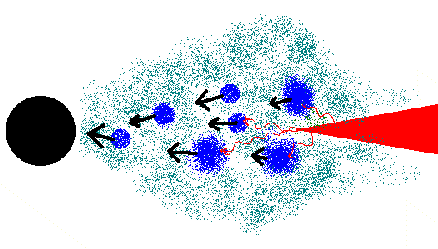
|
|
|
|
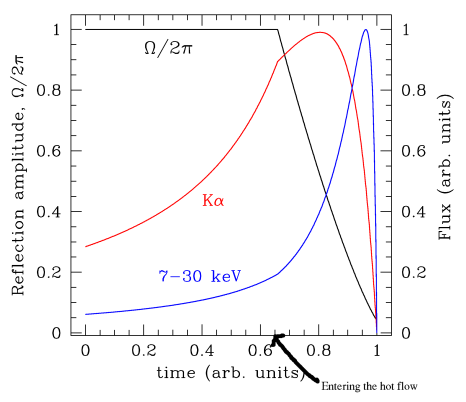
|
The decoupling
of line and continuum variability in the propagation model in the
disrupted disk geometry, are easy to understand. As an X-ray
emitting structure (“active region”) propagates
inwards, towards the central black hole, the X-ray flux
increases. Initially, when the structure is above the “solid”
part of the disk (red above),
the relative amplitude of reflection is 1 (solid angle
Omega=2pi). But when the structure
enters the region below truncation radius, the emitted continuum
flux still increases, but the reflection amplitude begins to
decrease – simply because the disk
“below” the structure is disrupted and so less
effective in reprocessing. Since the flux of the Kalpha line is
of course related to the amplitude, the flare of line
flux peaks earlier than the fluxes of the continuum,
and its amplitude is smaller. This is shown in the picture to the
left, but note that the fluxes (line
and continuum) were rescaled to 1 at
peak. So this plot does not show correctly the relative
amplitudes of the flare in the fluxes.
|
|
|
|
Now, it is a
relatively simple matter to compute a sequence of spectra (in the
same way as in previous project), and
extract the flux of the Kalpha line and that of e.g. 7-30 keV
continuum. Then, one can use the standard methods of
cross-correlation analysis to see how the two fluxes correlate
(or not), and compare those to correlations between two continuum
bands. Some of the results are shown to the right.
Generally, you
see reduced high-f variability (look at power spectra),
lack of coherence, and longer time lags between the line
and hard flux than timelags between two continuum bands.
Interesting, isn't it? (read
more)
|

|
top
Using Fourier frequency
resolved spectra to constrain the models of accretion
(Zycki,
2002, MNRAS, 333, 800, Zycki,
2003, MNRAS, 340, 639)
|
Two main classes of
geometries of accretion flows onto black holes are currently
considered: a standard accretion disk truncated at certain radius
and replaced by a hot, optically thin, geometrically thick flow
(possibly an ADAF), or the standard disk extending to the last
stable orbit, with either a dynamic corona or a hot skin. Each
model has to be able to explain a range of X-ray spectral
parameters (spectral slopes and amplitude of reflection), as well
as correlations between them (e.g. the R-Gamma correlation;
Zdziarski,
Lubinski & Smith 1999).
The question
is: is it possible to distinguish between the models (or at least
learn something new about them) using timing, or correlated
spectral-timing information?
|
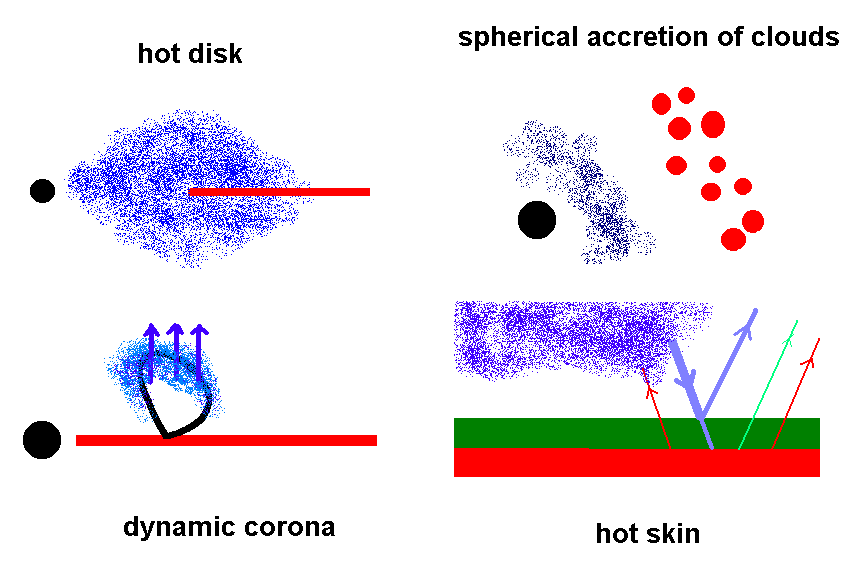
|
|
|
|

|
I have decided to use the
Fourier frequency resolved spectra for this purpose. The
f-resolved spectra are energy spectra computed in a
limited range of Fourier frequency (Revnivtsev,
Gilfanov & Churazov 1999).
That is, these are energy spectra of components varying on
different time scales. The observed spectra show interesting
dependence on f: the higher the frequency the harder the
spectrum and the smaller the amplitude of reflection.
|
A propagation
model in the disrupted disk geometry
(Zycki, 2003, MNRAS, 340, 639, ADS,
astro-ph (with color
figures))
|
In the geometry of an disrupted standard disk with inner hot
flow one can imagine that the X-ray emission is produced by some
sort of structures travelling from outside towards the center.
These could be compact active regions related to, for
example, magnetic reconnection and related particle acceleration
during the flow (see the paper by Bisnovatyi-Kogan
& Lovelace 2000). Alternatively, the active regions could
be micro-shocks forming in the hot plasma as it accretes onto the
center. Or, they could be global perturbations of the flow.
Whatever they are, assume that the X-rays are produced at a rate
roughly proportional to gravitational energy dissipation. A flare
of radiation is generated, with rather slow rise and very sharp
decay. As the flare progresses, the spectrum can be expected to
evolve from softer to harder, simply because the supply of soft
photons for Comptonization from the outer cold disk diminishes.
Simultaneously, the instanteneous amplitude of the reprocessed
component decreases, because the distant disk subtends smaller
and smaller solid angle. This spectral evolution is precisely
what is needed to produce the hard X-ray time lags (Kotov,
Churazov & Gilfanov 2001).
|

|
|
|
|
|
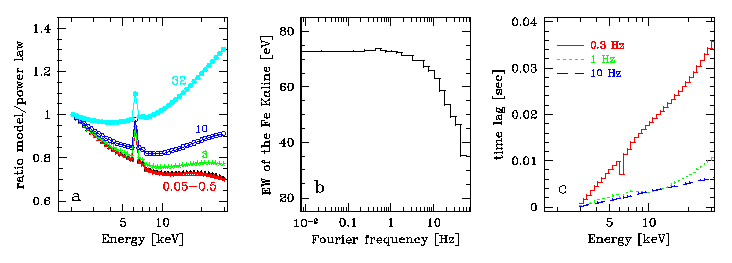
|
|
Given the geometry a number of observable quantities related
to time variability can be computed. So the plot above shows (a)
the f-resolved spectra (divided by a power law and normalized to
1 at 2 keV), (b) the equivalent width of the Fe Kalpha line as a
function of Fourier frequency, and (c) time lags as a function of
energy, for a number of Fourier frequency values. All of them
agree with what is observed.
|
Model of localized
magnetic flares
(Zycki, 2002, MNRAS, 333, 800,
ADS,
astro-ph)
|
I have combined the
variability model of Poutanen
& Fabian (1999) with
computations of the hot skin (see
below) to compute
the f-resolved spectra. The idea is that there is a unique
correspondence between the flare's time scale and its position on
the disk: fast (short lived) flares are located close to the
center, while slower flares are located farther away. Since all
parameters of the model of PF99 are uniquely specified if both
energy spectra and timing properties (PSD, time lags) are to be
quantitatively explained, so one can also uniquely compute the
thickness of the hot skin, as a function of time, radius etc. The
presence of the hot skin and a radial dependence of its thickness
introduce a radial dependence of energy spectra.
|
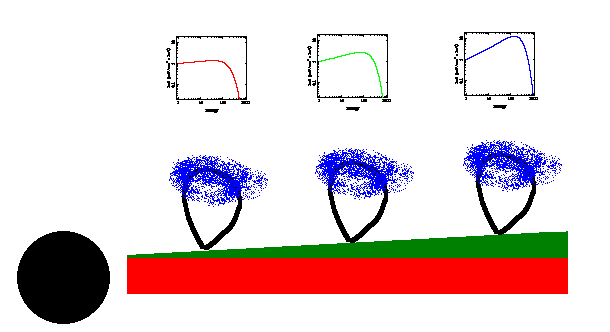
|
|
|
|
|
The computations give an
unexpected result: the (time averaged) thickness of the hot skin
increases with radius. This is because the
illuminating flux at the peak of a flare is the same for all
flares, so it is constant with radius. Since the gravity
decreases with radius, the thickness of the hot skin increases.
(The same value of the peak flux for all flares is an important
feature of the model and its modifications lead to wrong power
spectra.) As a consequence, the fast flares
(corresponding to high Fourier frequency)
produce intrinsically softer energy spectra
with larger amplitude of reflection.
The slower flares (corresponding to
low f) produce harder
energy spectra with smaller
amplitude of reflection. Correspondingly, the EW of the Fe
K line increases with frequency. These results are opposite to
what is observed in black hole binaries.
|
|
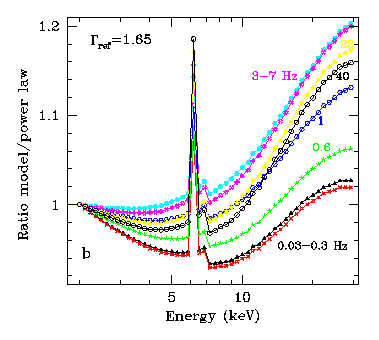
|
|
(see also seminar
talk I gave on the subject)
top
Variability of the Ka
line in AGN
(Zycki & Rozanska
2001, MNRAS, 325, 197. ADS
astro-ph)
|
A number of recent
observations of variability in AGN revealed that the Fe Kalpha
line is generally less variable than the X-ray continuum that
drives the line emission (E>7 keV). This would be possible if
e.g. the line originated far away from the central X-ray source,
since then the variability would be washed out. But the line is
generally broad (or at least contains a broad component), which
suggests that it originates close to the black hole (the
broadness is due to Doppler effects from a rotating accretion
disk). It was suggested that the lack of variability is caused
by complex ionization effects. Suppose that, as the X-ray flux
increases, the reprocessing medium gets ionized, so that the
efficiency of the line emission (I mean here neutral or weakly
ionized iron, as that is observed) per unit area decreases. It
is then possible that the line flux will remain roughly constant
in spite of the varying irradiation (see the plot to the right).
A physical realization of this idea involves the thermal
instability of X-ray irradiated plasma in hydrostatic
equilibrium. To make the long story short, such plasma can have
two stable states: relatively cold plasma (10^4 K) cooled by
atomic line emission, and hot plasma (10^7 K) heated and cooled
by the Compton process. The vertical structure of an irradiated
accretion disc is thus a two-zone structure: hot mostly ionized
layer ("hot skin"),
and the cool disk proper. The optical (Thomson) thickness of the
hot layer depends on the illuminating flux and is of the order
of 1, while its temperature varies from inverse Compton
temperature to (approximately) one third of it. With increasing
irradiation the thickness of such a hot skin increases, which
means the number of hard X-ray illuminating photons penetrating
to the cold disk decreases (the hot skin is almost purely
scattering atmosphere). As a consequence the efficiency of Fe
Kalpha line production (the number of line photons per continuum
photon) decreases. We wanted to test this qualitative argument
by actual computations.
|
|
|
|
|
|
We computed the structure
of the hot skin and underlying disk (the hot skin thickness does
depend on the disk structure), as a function of irradiating
flux. The conclusion is that is the flux increases by a certain
factor, the thickness obviously does increases somewhat. This
leads to a decrease of the line efficiency, which is however not
sufficient to compensate the increase of the irradiation
flux. The flux of line photons then does increase as a response
to increased irradiation. If the irradiation flux is correlated
with observed (no anisotropy), we cannot observe constant line
flux when the continuum varies. There were later claims that the
Fe line does vary on short time scales in MCG-6-30-15, but the
variability is not easily related to the continuum variability.
Perhaps the hot skin has some effect on the response of the line
(well it surely should have), but it's not trivial - for example
Sergei Nayakshin noticed that the adjustment of hydrostatic
equilibrium when the medium is suddenly illuminated by a strong
X-ray flux is relatively slow (on dynamical time scale). During
the time the flux can change again, so the medium may be in a
state not determined by the instantaneous X-ray flux.
|
|
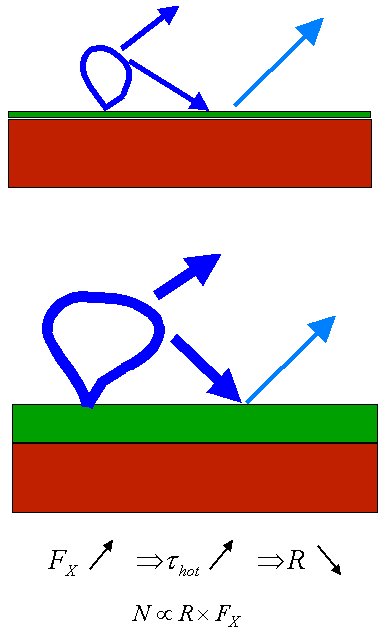
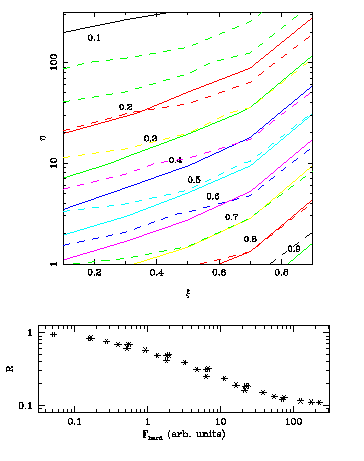
In
upper panel the dashed contours represent X-ray flux, F - each
contour means twofold increase of the flux. The solid (labelled)
contours represent the relative amplitude of reflection, R. You
can see that to get a decrease of R by e.g. a factor of 2, the
flux must increase by much more than the factor of 2. This means
that the flux of line photons, N \propto R * F, will not be
constant when F changes
|
top
Analysis of X-ray spectra of
Soft X-ray Transients in their soft states.
(Zycki,
Done & Smith, 2001, MNRAS, 326, 1367. ADS
astro-ph)
|
Soft X-Ray
Transient (SXT) sources are a subclass of X-ray binaries
occasionally undergoing dramatic outbursts (factor of 10^6 or
even more). There is a great deal of interest in them, since
they allow studying the accretion flows as a function of
accretion rate, which seems to be the most important parameter.
Of particular interest are those objects which contain black
holes, as black holes are "cleaner" accretors than
neutron start (no global magnetic field), and they are even more
'exotic' than neutron stars. Above certain accretion rate (in
Eddington units) the X-ray spectra (let's say above 1 keV)
contain a strong soft thermal component - hence such spectral
states can be call "soft states". There is also a hard
tail, relatively steep (Gamma>2, so it's actually fairly
'soft' but I'll call it 'hard' to distinguish it from the soft
thermal component), of varying strength (from none to roughly
equal to the soft component). In literature these states are
named "intermediate state", "high state" or
"very high state", depending on the relative strength
of the hard component. The spectrum of the soft component is
close to a (disk) blackbody, so the component is thought to come
from an accretion disk. The hard component is roughly a power
law, so is thought to be Comptonization of the disk photons by
energetic electrons with a thermal or non-thermal energy
distribution.
|
|
|
|
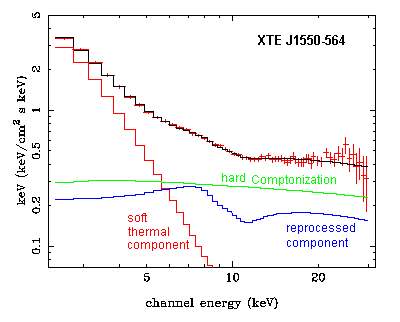
We
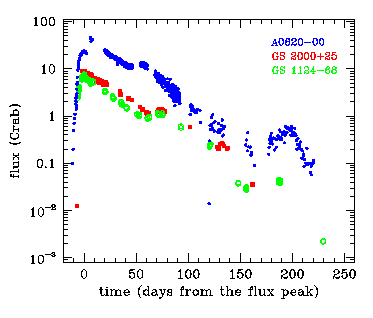
analyzed a number of data sets from archives, from old Ginga and
newer RXTE satellites, for objects like GS 2000+25, GS 1124-68,
GRO J1655-40, XTE J1550-564. This was of course not the first
time that those data were analyzed, but we paid a bit more
attention to the process of modeling, than was usually done
before. First, in many papers the spectral features near 5-9 keV
are modeled using so called 'smeared edge' model. That was
useful 8-10 years ago when it was introduced, but even then K.
Ebisawa remarked that the only reason to use it is that a
proper, computationally efficient model of X-ray reprocessing
did not exist. There is no such excuse now, when good models of
reprocessing are available. In particular, it is important
to use models which consistently compute
the Compton-reflected continuum and the Fe Kalpha line.
Second,
a simple power law is not the ideal model for the hard tail, if
this is due to Comptonization of the soft photons from the
thermal component: one has to use a model that includes the low
energy cutoff (at the seed photons temperature about 1 keV) in
the Comptonized spectrum.
|
|
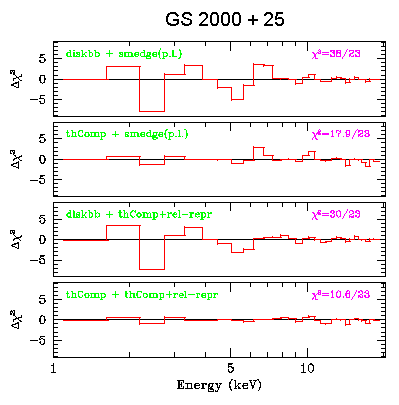
Residuals
from a sequence of fits to Ginga data of GS 2000+25,
showing that the best fit model (lowest panel) has a Comptonized
soft component, second hard Comptonized component and its
reprocessed component.
|
|
There are two
main conclusions from modeling a number of spectra:
1.
the soft component seems to be more complex than previously
thought. Phenomenologically, we can describe it either as a sum
of a disk blackbody and an additional blackbody, or as a
Comptonized blackbody (the data are not good enough to
distinguish the two possibilities). So how do we interpret the
two possibilities?
The first
could be that the disk blackbody is the usual thermal emission
from the accretion disk, while the additional blackbody comes
from hotter spots on the disk. The hot spots would be areas
close to magnetic flares, illuminated by the hard X-rays (the
hard tail) produced in the flares. If the flares are
relatively compact (as they seem to be, Nayakshin &
Kallman 2001), the illuminated area is relatively small and
its temperature relatively high.
The second
possibility - Comptonized blackbody - would mean that the
vertical structure of the disk is not trivial. For example the
disk could have a hot skin (but rather thicker than what we
considered in previous project! - Thomson thickness about 10),
and so the soft photons coming from the disk interior would be
additionally Comptonized
Another
related possibility is that the Comptonizing plasma has hybrid
energy distribution of electrons (see the paper
by P. Coppi). The low energy electrons have a Maxwellian
distribution, so they do the low temperature thermal
Comptonization, while the high energy electron have a power
law (non-thermal) distribution, producing a power law photon
spectra
2.
the proper reprocessed component very well describes the
spectral features near 5-9 keV - no need for 'smeared edge' and
gaussian line. The reprocessed component is highly ionized
(that's what we would expect considering that the disk
temperature is a good fraction of 1 keV - or even more). It
also seems to be additionally smeared - that means the spectral
features are even broader that what we would expect from
superposition of a number of degrees of ionization. That
suggests Doppler effect from the accretion disk, although it
should be remembered that Comptonization of the spectral
features, as the photons diffuse to the surface, is not
properly modeled by most models of reprocessing. This may
affect the results of spectral fitting. On the other hand, it's
difficult to imagine that the reprocessor is so hot and
located so far away from the center that the Doppler effect is
unimportant
|
|
top
Properties of the X-ray
reprocessed component in accreting black hole systems in low/hard
spectral state
Zycki,
Done & Smith, 1997, ApJ, 488, L113
Zycki,
Done & Smith, 1998, ApJ, 496, L25
Zycki,
Done & Smith, 1999, MNRAS, 305, 231
Done
& Zycki, 1999, MNRAS, 305, 457
Done,
Madejski & Zycki, 2000, ApJ, 536, 213
Di
Salvo, Done, Zycki, Burderi, Robba, 2001, ApJ, 547, 1024
|
|
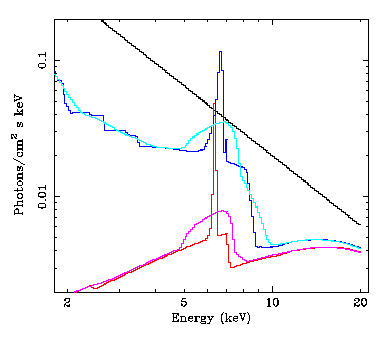
In
these papers we analyzed a number of X-ray data sets from various
objects (1., 3.- SXT GS 2023+338; 2.- SXT
GS 1124-68; 4., 6.- Cyg X-1,
5. - Seyfert 1 IC 4329a) to try to
characterize the X-ray reprocessed component. The reprocessed
component consists of the Compton reflected continuum and
spectral features superimposed on it. Of these spectral features
the Fe Kalpha line and Fe K-shell absorption edge (roughly at 6-9
keV) are most prominent. Assuming the simple reprocessing model
(uniform
constant density medium) the properties of the line
and the continuum are uniquely related. That is, when you've
specified all the parameters needed to compute the reflected
continuum, the Kalpha line is uniquely determined (so its energy,
or energies of its components, and intensity is determined).
Well, that is obvious if we think about it from the point of view
of atomic physics. It is perhaps less obvious how to construct a
good, computationally efficient model of such a reprocessed
component. That is probably why the most popular reflection
models implemented in XSPEC (pexrav
and pexriv
constructed by Magdziarz
& Zdziarski; 1995) compute only the reflected continuum
without the line. But simply adding to the continuum a gaussian
line to account for the Kalpha line is not
a good solution, since there is no way to ensure
the consistency of the properties of the continuum and the line.
It certainly did not work for us especially when the
reprocessing was ionized and e.g. the energy of the line could
not be fixed in the fitting procedure. So we implemented the
model which computed the line consistently with the reflected
continuum. The line was computed as in Zycki
& Czerny (1994), with photoionization computations as in
Done
et al. (1992; the same code which is used in pexriv). We also
added the possibility that the spectral features are broadened by
Doppler effects and gravitational redshift, if they come from a
rotating accretion disk (using the prescription from Fabian
et al. 1989). Such a model has fewer free parameters than the
"smeared edge" plus broad gaussian line model, and of
course is superior to the latter since the parameters have
physical meaning. And the reprocessed component can be computed
for any (reasonable) primary continuum spectrum. Well, that much
for the propaganda. The model is available for downloading here.
|
|
|
|
The results of
modeling many datasets of various source (but all of them were in
the low/hard state) was that:
The
reprocessed component is there, or, when the characteristic
broad residuals are seen near 5-9 keV when you've fitted a power
law to your data, the residuals can always be fitted by the
reprocessed component.
In
low/hard state the reprocessed component is rather weakly
ionized and its amplitude is less than 1 (where 1 means an
isotropic source above a flat infinitely extended disk).
The
spectral features are additionally broadened ("smeared").
The smearing can be interpreted as the kinematic/relativistic
effects from an accretion disk, but the inner radius of the disk
is larger that the last stable orbit at 6 Rg (=6GM/c^2). This
means that the reflecting disk does not go all the way to the
last stable orbit, contrary to what we might expect.
These results
are consistent with the idea that the accretion disk is truncated
at somewhere between 20Rg and 100Rg, and, let's say, replaced by
a hot X-ray producing flow (possibly an ADAF), but this is not a
unique interpretation (see for example Di
Salvo et al. 2001).
|
|
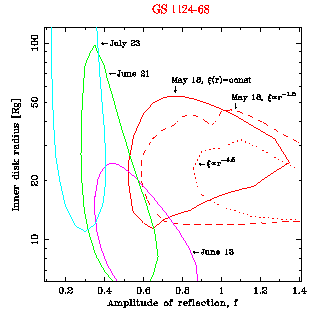
In GS 1124-68
(Nova Muscae 1991, paper
2.) we analyzed a number of datasets, which covered a part of
the decline phase of the source outburst, namely a soft state,
and the transition to the hard state. Very nice result that we
obtained for the transition is that there is an evolution of not
only the primary continuum, but also of the reprocessed
component. Its amplitude decreases with
time, and its ionization drops
suddenly when the soft-to-hard transition takes place. The
results for relativistic smearing were not unique. They were
consistent with both an increasing value of the inner radius of
the reflecting disk, but a constant Din could also describe the
data. Overall then, these results were consistent with a
retreating inner disk as the accretion rate was decreasing, in
qualitative agreement with the ADAF-based models, but
quantitatively the radii we derived were much smaller than those
proposed in the ADAF papers.
|
|
|
|
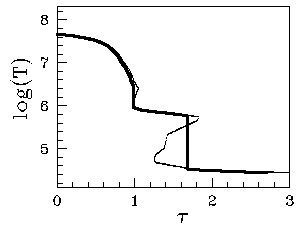
The atmosphere
of an illuminated accretion disk is unlikely to have a constant
density. X-ray illuminated plasma under the condition of
hydrostatic equilibrium is subject to the thermal
instability. This makes the vertical structure of such disks
quite complex, and computations of the reprocessed spectra from
them very difficult. Computations of the vertical structure and
resulting spectra were done by Agata Rozanska with collaborators
and a good working model of the reprocessed component, ready for
implementing into XSPEC, was constructed by S. Nayakshin. But the
precise geometry of the reprocessor is still uncertain and it's
not obvious a priori, which approximation (constant
density of hydrostatic equilibrium) may be more appropriate.
Whichever you choose, do it consistently.
|
![]()